Shooting on an angle? These tips will keep you on target

Had I known the lessons would come in handy later in life while hunting, I would have paid much more attention in high school to Mr. Bilous’s trigonometry class. That’s especially the case when it comes to trying to remember whether to aim higher or lower when shooting at steep uphill or downhill angles—and why.

Let’s get to the answer before we talk math and physics. To begin with, don’t worry about adjustments if you’re within 100 metres of your target, or if you’re shooting at a gentle up or down angle, as the difference in the point of impact won’t be significant. However, if you’re shooting at steep angles at extended ranges, whether uphill or downhill, you’ll need to aim lower than you normally would for that same line-of-sight distance.

That answer seems counterintuitive, and that’s what leads to confusion, turning a simple problem into one more complex than it needs to be. This is where Mr. Bilous and his math and physics come into play.

THE COMPLICATED CALCULATIONS

What you must remember is that a bullet’s flight path, or trajectory, is influenced by gravity. If there were no gravity, a bullet would, theoretically, have a completely flat trajectory. But gravity tugs downward on a bullet throughout its horizontal path, and that is key to understanding the issue of shooting low at steep angles.

Let’s take the example of an elk standing on a ridge 300 metres away at a 60-degree uphill angle. To make the shot, you first need to calculate the horizontal distance to the elk. That requires determining the cosine (ugh, trigonometry!) of the right-angled triangle formed between you, the elk and the vertical difference between you and the elk (the same would apply if the elk were below you).

So, if you work through the formulas, you will learn that the actual horizontal distance is only about half the 300-metre line-of-sight distance, or roughly 150 metres. That means you need to aim at the elk as though it were 150 metres away. Otherwise, if you aimed as though it were 300 metres away, you’d end up shooting high. At extended distances or extreme angles, that can mean the difference between a hit and a miss, or worse, a poor hit and a wounded animal.

That’s a lot of math, however, and none of us has the time or inclination to work through such complex formulas when we’re in the field. So, is there an easier solution?

[easy-tweet tweet=”@OutdoorBailey explains the easy way to calculate those pesky adjustments for shooting’s ups and downs” user=”OutdoorCanada” hashtags=”hunting, shooting, firearms, deerhunting”]

THE SIMPLE SHORTCUT

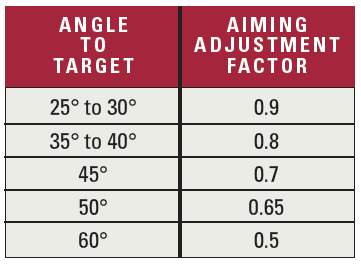
As it turns out, there is indeed a much simpler way to calculate the horizontal distance to a target above or below you, and as far as I can determine, it originated from the bright minds at the FBI. They did all the tricky math, then developed the handy table below for quickly making the final calculation.

Here’s how it works. First, estimate the line-of-sight distance to your target (or better yet, use a rangefinder), then estimate the angle to the target. Now simply multiply the line-of-sight distance by the table’s aiming adjustment factor that corresponds to the angle. For example, if the line-of-sight distance to a sheep is 500 metres, and you estimate it’s below you at a 45-degree angle, you would multiply 500 by 0.7 to get the horizontal distance of 350 metres. Again, that means you must aim at the sheep as though it were 350 metres away, not 500, or you will most likely miss.

It’s worth noting that most people have a tendency to overestimate the angle at which they’re shooting. Even a 45-degree slope is very steep, so it generally pays to be a little conservative when estimating angles. It’s also worth pointing out that compensating for gravity’s influence on your bullet’s trajectory when shooting at an angle doesn’t have to be complicated. Just remember that you’re always going to be aiming as though you’re closer to your quarry than the actual line-of-sight distance. It’s really just that simple.